At least ten percent increased all-cause mortality in high-vaccination countries

Analyses from 39 countries with over a billion inhabitants show that per capita corona vaccination doses explain nearly 57 percent of the variation in all-cause excess mortality, with a beta value of .75 (1 is a perfect correlation). A conservative estimate is a ten percent higher mortality rate in high-vaccination countries than in low-vaccination countries.

Vaccination doses and excess mortality are the weekly averages from the beginning of March 2022, approximately when the rollout leveled off, and through 2023. The analyses are weighted for differences in population size.

Are there alternative explanations? No. The study has controlled for countries’ accumulated excess mortality, socioeconomic development, median age, and population size.

During the rollout, around the latter half of 2021 and early 2022, vaccination may have provided some protection since mortality was relatively low in countries with high vaccination rates. However, the pattern was similar for mortality excluding corona-related deaths, and there is accordingly reason to question the temporary protection.

Norwegian version here.

Before the flattening of the vaccination rate

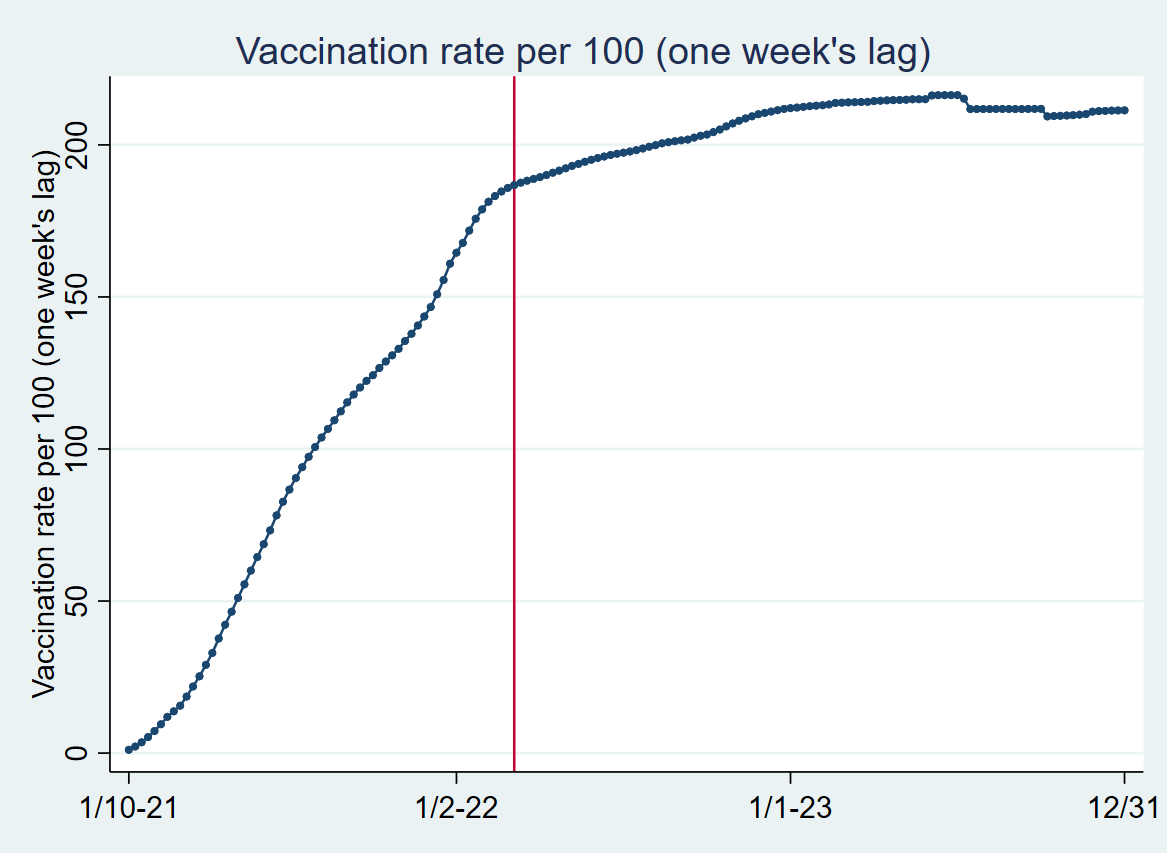
Graph 1 shows weekly associations between log-transformed per-capita vaccination coverage and the percentage of all-cause excess mortality in 39 countries from January 10, 2021, to 2023 (1). The red horizontal line has been included to highlight values ​​above and below zero. The red vertical line shows the point in time when vaccine rollout roughly leveled off around March 6, 2022, i.e., the change with a one-week lag was less than one percent (2).

At the very beginning of the vaccine rollout, where the elderly and comorbid were prioritized, we observed higher mortality in countries that have given the most doses per capita. The trend is consistent with a Norwegian study concluding that for nursing home residents, the vaccine “may in a few cases have contributed to accelerating an ongoing death process” (my translation).

From around the latter half of 2021 and the beginning of 2022, we see that excess mortality was markedly and significantly lower the higher the vaccination rate (3). This may indicate a protective vaccine effect, but Graph 2, which adds data where corona-related deaths are excluded, highlighted in purple, shows a fairly large coincidence with all-cause excess mortality (4). Since the corona vaccine does not protect against corona-unrelated deaths, I conclude that negative associations in the relevant period largely cannot be attributed to the vaccine. However, the negative association is somewhat less for corona-unrelated mortality and may accordingly indicate some temporary protection.

From around March 6, 2022, marked by the vertical line, i.e., when the vaccine rollout roughly leveled off, we consistently observe a positive association between vaccination coverage and excess mortality, significant in most weeks. The picture is the same for excess mortality, excluding corona-related deaths. This period is the subject of analyses that I will explain below.

Graph 1.

Graph 2.

After the flattening of the vaccination rate

Graph 3 (as illustrated at the top) shows the relationship between the 39 countries’ average all-cause excess mortality and average per-capita vaccination rate. The average values ​​are measured from March 6, 2022, which I have pointed out was approximately when the vaccine rollout leveled off, through 2023. The red regression line, weighted for population size, e.g., the USA is weighted more in the analyses than Iceland, has a regression coefficient of .076 (5). I.e., a one percentage point increase in per-capita vaccination gives a .076 percentage point higher mortality. A conservative estimate is ten percent higher mortality in high-vaccination countries than in low-vaccination countries from the beginning of March 2022 to the end of 2023, almost two years.

The P-value, i.e., the significance value, is well below .001 (where .05 is usually considered “significant”). Different vaccination rates between countries explain nearly 57 percent of the variation in all-cause excess mortality. The beta value is close to .75 (1 is a perfect correlation).

Are there alternative explanations? No. The study has controlled for different countries’ accumulated excess mortality, socioeconomic development, median age, and population size (6).

Graph 3.

Notes

1. The data for the analyses is Our World in Data. The dataset is extensive, but there are major shortcomings in many countries. There may also be reason to assume that the data quality for perhaps particularly some developing is relatively poor. Comparing countries that are very different in socioeconomic development can also be problematic. I have therefore taken as a starting point countries that were ranked “Very high” on the Human Development Index scale by the UN in 2019. This indicates relatively good data quality, as well as relatively homogeneous data. Our World in Data contains consistent data over time from 39 of these countries, which I therefore used in the analyses (for other countries, there were no data to be included in the analyses I present in the graph). 32 are European, while the remaining are Canada, the USA, Chile, Australia, New Zealand, South Korea, and Israel (where I have taken data after the outbreak of the war). The total population in the 39 countries is just over one billion. Some countries reported weekly data on different days, and to synchronize, I rounded to the nearest Sunday. Vaccination rate is the number of doses per 100 inhabitants per country. For example, if the vaccination rate for a country in week 10 was 50 and 56 in week 13, the vaccination rate in week 11 was estimated to be 52 and 54 in week 12 in case of missing observations. The last observation on the vaccination rate for a country was used in the remaining analyses. In all analyses, the vaccination rate was included with a one-week lag. Log-transformation of vaccination rate provides better information about changes in vaccination during rollout. For example, changes from 10 to 10.1 and 100 to 101 both give a one percent increase in vaccination rate. Log transformation also reduces problems with multicollinearity. Karlinsky and Kobak provide detailed information on how excess mortality is measured. Specifically, I use robust regression with cluster-adjusted error terms, i.e., the method allows for dependence between error terms within countries. This is relevant since the same country is included over time. The analysis includes interaction terms between the vaccination rate and the time variable (dummies). Although multicollinearity cannot be ruled out, separate weekly measurements give the same conclusion as the graph shows. All analyses were done in Stata.

2. Except for one week later when we observed an increase of just over one percent. For a visualization of the vaccine rollout, see the graph below. Unnatural changes at the end are due to countries not being included in certain weeks.

3. Weekly values ​​below zero show negative associations. This means that excess mortality tends to be lower the higher the vaccination rate. Significant means that the upper (lower) 95 percent confidence interval is below (above) zero for negative (positive) associations. The graph visualizes 95 percent confidence intervals with “tags.” Since the vaccination rate is log-transformed, it means that if the y-axis shows –50, for example, a one percent increase in vaccination rate is associated with approximately .5 percent reduction in mortality.

4. I have estimated (a) excess mortality excluding corona-related deaths by using (b) weekly changes in cumulative excess mortality per million, (c) the smoothed curve in corona-related deaths per million per week, and (d) the original measure of excess mortality in the following equation: a=d*(b–c)/b. For two weeks, the relationship between vaccination rate and excess mortality unrelated to corona gave large negative results. The reason is follow-up reporting of corona-related deaths and cumulative excess mortality in some weeks. Absent this, the possible temporary vaccine protection I have alluded to would have shown a lower magnitude.

5. 95 percent confidence intervals with robust standard errors range from .047 to.104.

6. The variable population size is log-transformed since a population change of, for example, 10,000 is more important in a small than a large country.